Une plongée profonde dans l’autorégression vectorielle dans R – Justin Eloriaga

Laissez parler les données! Purgeons les attentes a priori.

Christopher Sims a proposé la Vector Autoregression qui est un modèle de séries chronologiques linéaires multivariées dans lequel les variables endogènes du système sont des fonctions des valeurs décalées de toutes les variables endogènes. Cela permet une alternative simple et flexible au système structurel traditionnel d’équations. Un VAR pourrait modéliser les données macroéconomiques de manière informative, sans imposer de restrictions ou de relations très strictes. Il s’agit essentiellement d’une modélisation macroéconomique sans a priori les attentes se mettent en travers.

Les VAR sont très utiles, en particulier dans le domaine de la macroéconomie. Il a été largement utilisé pour simuler les chocs macroéconomiques sur l’économie réelle et a été largement utilisé dans les simulations et les prévisions politiques. Il s’agit de la poussée et de l’utilisation principale de l’autorégression vectorielle. Tout d’abord, c’est un outil de prévision. Nous montrerons comment les VAR peuvent être bien meilleurs que les modèles de prévision univariés standard, en particulier pour déterminer le long terme. La majorité des études empiriques sur les prévisions suggèrent que le VAR a déjà éclipsé les modèles de prévision univariés traditionnels et les modèles d’équations structurelles fondés sur la théorie.

Outre les prévisions, les VAR sont également des outils utiles pour analyse structurale. Nous notons que les VAR peuvent enquêter sur la réponse aux chocs. Il peut identifier les sources de fluctuations auxquelles les modèles univariés traditionnels échouent. De plus, les VAR peuvent aider à distinguer les modèles théoriques concurrents.

Comme nous l’avons mentionné précédemment, le VAR est un modèle de séries chronologiques linéaires multivariées où les variables endogènes dans le système sont des fonctions des valeurs décalées de toutes les variables endogènes. Autrement dit, le VAR est essentiellement une généralisation du modèle autorégressif univarié. Généralement, nous notons un VAR comme un VAR (p) où p indique le nombre de retards autorégressifs dans le système. Considérons un système VAR avec seulement deux variables.

Nous pouvons également écrire ceci sous forme de matrice comme

L’estimation d’un VAR est un Équation par équation OLS. Nous exécutons essentiellement OLS sur chaque équation. Nous constatons que les estimations sont cohérentes car seules les valeurs décalées des variables endogènes se trouvent à droite de l’équation. De plus, les estimations sont également efficaces dans la mesure où toutes les équations ont des régresseurs identiques, ce qui minimise la variation dans chacune d’elles. Faire cela suggère qu’il est essentiellement équivalent à un moindres carrés généralisés. L’hypothèse d’une corrélation sans série est également valable à cet égard.

Nous allons maintenant appliquer les nombreux concepts appris en VAR dans un exemple réel. En particulier, nous utiliserons un cadre développé par Sims (1992) à partir de données philippines. Dans ce modèle, nous utiliserons quatre variables. Ce sont les suivants:

Taux de rachat inversé de nuit (RRP) qui est fixé par le Bangko Sentral ng Pilipinas. Il s’agit, selon tous les comptes, du principal taux directeur contrôlé par la banque centrale des Philippines.

M1 Money Supply qui peut être obtenu sur le site Web du BSP

Taux d’inflation IPC qui est communiqué mensuellement par la Philippine Statistics Authority et mesure l’augmentation relative des prix sur la base d’un indice des prix de Laspeyres.

Production industrielle qui mesure la valeur de tous les biens du secteur industriel.

Nous allons d’abord estimer un VAR standard qui reflète une réponse économique clé. On pense en théorie et par Sims que les chocs sur le taux d’intérêt nominal représentent des chocs de politique monétaire. Un choc sur la variable politique affecte simultanément toutes les autres variables. La variable est affectée par toutes les autres au cours de la période et est classée en dernier. Enfin, la banque centrale n’observe que des variables non politiques avec un décalage.

Nous recommençons par installer les packages requis et les charger à l’aide de la commande library (). Pour cette partie, nous devons installer le package «vars» qui aura une multitude de commandes nécessaires pour exécuter le VAR et le SVAR et les tests de diagnostic et les applications à suivre. Nous voyons ensuite les graphiques de chaque variable et jugeons certaines conditions initiales telles que la non-stationnarité.

Comme nous l’avons dit, nous devons installer le package «vars». Utilisez la commande install.packages («vars») pour ce faire. Après cela, nous chargerons ce package avec notre suite standard de packages et de bibliothèques pour que nous puissions continuer l’estimation.

install.packages("vars")
library(vars)
library(mFilter)
library(tseries)
library(TSstudio)
library(forecast)
library(tidyverse)

Après l’installation et le chargement, il est temps de charger notre jeu de données. Nous utiliserons le fichier Sample_VAR.csv qui contient les données sur toutes les variables de janvier 2003 à février 2020. Les données sont mensuelles et accessibles au public, obtenues auprès du BSP et du PSA. Nous utilisons la commande read_csv () pour lire l’ensemble de données et la commande file.choose () pour ouvrir une boîte de dialogue nous permettant de sélectionner nos données. Dans ce cas, nous plaçons l’ensemble de données sous un objet nommé «mp». Nommez-le comme vous le souhaitez, si vous le souhaitez. Nous utilisons ensuite la commande head () pour voir les premières lignes de l’ensemble de données afin de vérifier s’il s’est correctement chargé. Les fichiers et le code peuvent être trouvés ici: https://drive.google.com/drive/u/0/folders/11mAXh0trxjuf1y_yh-AJXgxulHQwcBEn

mp <- read_csv(file.choose()) 
head(mp)

Ensuite, nous devons déclarer chaque variable dans l’ensemble de données comme une série temporelle à l’aide de la commande ts (). Nous utilisons le symbole $ pour appeler une variable de l’ensemble de données. Toutes les variables commencent en 2003 avec le même jour et le même mois de janvier. Nous avons fixé la fréquence à 12 car nous avons affaire à des données mensuelles.

lnIP <- ts(mp$lnIP, start = c(2003,1,1), frequency = 12)
M1 <- ts(mp$M1, start = c(2003,1,1), frequency = 12)
CPI <- ts(mp$CPI, start = c(2003,1,1), frequency = 12)
RRP <- ts(mp$RRP, start = c(2003,1,1), frequency = 12)

Nous pouvons également visualiser notre série en utilisant la commande autoplot () ou ts_plot (). Comme précédemment, la commande ts_plot () est une version plus interactive utilisant le package plot.ly comme base.

ts_plot(lnIP)
ts_plot(M1)
ts_plot(CPI)
ts_plot(RRP)

Encore une fois, il est important d’évaluer si les variables à l’étude sont stationnaires ou non. Comme nous l’avons dit, avoir des variables stationnaires est un cas idéal dans notre VAR même si nous pouvons l’exécuter sans celles-ci. Comme nous y sommes habitués, utilisons les tests que nous connaissons. Pour plus de simplicité, nous utiliserons le Phillips Perron afin que nous n’ayons pas besoin de spécifier le nombre de décalages.

pp.test(lnIP)
pp.test(M1)
pp.test(CPI)
pp.test(RRP)

Dans l’estimation ci-dessus, nous constatons que toutes les variables sont des variables non stationnaires. N’oubliez pas qu’un rejet de l’hypothèse nulle suggère que les données sont stationnaires. Néanmoins, nous pouvons toujours exécuter une estimation VAR en utilisant ces données de niveau. Cependant, vous pouvez choisir de différencier les données et voir si cela fournit de meilleurs résultats et prévisions.

Le moment est venu d’estimer formellement notre VAR. Nous devrons d’abord lier nos variables VAR ensemble pour créer le système. Après cela, nous sélectionnerons l’ordre de décalage optimal derrière le VAR que nous utiliserons. Nous exécuterons ensuite une estimation VAR sans restriction et verrons les résultats. Enfin, nous exécuterons des diagnostics tels que des tests d’autocorrélation, de stabilité et de normalité.

La première étape consiste à construire le système VAR. Cela se fait via la commande cbind () qui regroupe essentiellement nos séries chronologiques. Nous allons commander ceci dans l’ordre souhaité que nous jugeons approprié. Nous l’enregistrerons dans un objet appelé «v1». Nous renommerons ensuite les variables en liste à suivre en utilisant la commande colnames ().

v1 <- cbind(RRP, lnM1, CPI, lnIP)
colnames(v1) <- cbind("RRP","M1","CPI", "lnIP")

Après avoir lié les variables et créé le système VAR, nous déterminerons un ordre de retard que nous utiliserons. Pour ce faire, nous utilisons la commande VARselect () et utilisons l’objet v1 que nous venons de créer. Nous utiliserons un ordre de décalage maximum de 15. La commande générera automatiquement l’ordre de décalage préféré basé sur les itérations multivariées de l’AIC, du SBIC, du HQIC et du FPE.

lagselect <- VARselect(v1, lag.max = 15, type = "const")
lagselect$selection

L’exécution des commandes suggère que l’ordre de décalage à utiliser est 2. Dans l’étude des Sims, il a utilisé 14 décalages qui pourraient être plus adaptés aux données américaines car les effets reflètent une plus grande persistance.

Nous allons maintenant estimer un modèle. Nous estimons le VAR à l’aide de la commande VAR (). L’option p fait référence au nombre de retards utilisés. Étant donné que nous avons déterminé que 2 retards sont les meilleurs, nous avons défini ce paramètre à 2. Nous le laissons être un VAR sans restriction typique avec une constante et nous ne spécifierons aucune variable exogène dans le système. La commande summary () répertorie les résultats.

Model1 <- VAR(v1, p = 2, type = "const", season = NULL, exog = NULL) summary(Model1)

Nous n’interprétons généralement pas les coefficients du VAR, nous interprétons généralement les résultats des applications. Vous verrez cependant que nous avons là des coefficients pour chaque décalage et chaque équation dans le VAR. Chaque équation représente une équation dans le système VAR.

Une hypothèse est que les résidus devraient, autant que possible, être non autocorrélé. C’est à nouveau sur notre hypothèse que les résidus sont du bruit blanc et donc non corrélés avec les périodes précédentes. Pour ce faire, nous exécutons la commande serial.test (). Nous stockons nos résultats dans un objet Serial1.

Serial1 <- serial.test(Model1, lags.pt = 5, type = "PT.asymptotic")Serial1

Dans ce test, nous voyons que les résidus ne montrent aucun signe d’autocorrélation. Cependant, il y a une chance que si nous changeons l’ordre de décalage maximum, il pourrait y avoir un signe d’autocorrélation. En tant que tel, il est préférable d’expérimenter avec plusieurs ordres de décalage.

Un autre aspect à considérer est la présence de hétéroscédasticité. Dans les séries chronologiques, il y a ce que nous appelons Effets ARCH qui sont essentiellement des zones de volatilité regroupées dans une série chronologique. Ceci est courant dans les séries telles que les cours des actions où des hausses ou des baisses massives peuvent être observées lors de la publication d’un appel de bénéfices. Dans cette zone ou fenêtre, il pourrait y avoir une volatilité excessive modifiant ainsi la variance des résidus, loin de notre hypothèse de variance constante. Nous avons des modèles pour les prendre en compte, qui sont les modèles de volatilité conditionnelle dont nous discuterons dans une section ultérieure.

Arch1 <- arch.test(Model1, lags.multi = 15, multivariate.only = TRUE)Arch1

Encore une fois, les résultats du test ARCH ne signifient aucun degré d’hétéroscédasticité car nous ne parvenons pas à rejeter l’hypothèse nulle. Par conséquent, nous concluons qu’il n’y a pas d’effets ARCH dans ce modèle. Cependant, comme avec le test d’autocorrélation, il est possible d’enregistrer les effets de décalage lors des ordres de décalage suivants.

Un pré-requis doux mais souhaitable est la normalité de la distribution des résidus. Pour tester la normalité des résidus, nous utilisons la commande normality.test () dans R qui apporte le test de Jarque-Bera, le test de Kurtosis et le test de Skewness.

Norm1 <- normality.test(Model1, multivariate.only = TRUE)Norm1

D’après les trois résultats, il semble que les résidus de ce modèle particulier ne soient pas normalement distribués.

Le test de stabilité est un test de la présence de ruptures structurelles. Nous savons que si nous ne sommes pas en mesure de tester les ruptures structurelles et s’il y en a eu une, toute l’estimation peut être rejetée. Heureusement, nous avons un test simple pour cela qui utilise un tracé de la somme des résidus récursifs. Si, à n’importe quel point du graphique, la somme sort des limites critiques rouges, alors une rupture structurelle à ce point a été observée.

Stability1 <- stability(Model1, type = "OLS-CUSUM")plot(Stability1)

Sur la base des résultats du test, il ne semble pas y avoir de rupture structurelle évidente. En tant que tel, notre modèle passe ce test particulier

Nous allons maintenant passer aux simulations de politiques dans un VAR régulier. Nous en ferons les trois principales, qui sont la causalité de Granger, la décomposition de la variance des erreurs de prévision, ainsi que les fonctions de réponse impulsionnelle.

Nous allons tester la causalité globale de Granger en testant chaque variable du système par rapport à toutes les autres. Comme nous l’avons dit, il pourrait y avoir une relation de causalité unidirectionnelle, bidirectionnelle ou inexistante entre les variables.

GrangerRRP<- causality(Model1, cause = "RRP")
GrangerRRPGrangerM1 <- causality(Model1, cause = "M1")
GrangerM1GrangerCPI <- causality(Model1, cause = "CPI")
GrangerCPIGrangerlnIP <- causality(Model1, cause = "lnIP")
GrangerlnIP

La commande utilisée convient aux cas bivariés mais nous allons l’utiliser dans un système de quatre pour l’instant. Certains d’entre vous peuvent essayer de réduire les modèles VAR à deux variables pour voir des interprétations plus simples. Pour effectuer le test de causalité de Granger, nous utilisons la commande causality (). Sur la base des résultats, nous concluons que l’IPC Granger provoque les autres variables mais l’inverse n’est pas vu. Peut-être que des relations granulaires de variable à variable plutôt que de variable à groupe s’avéreraient plus importantes.

Nous allons maintenant passer à nos fonctions de réponse impulsionnelle. Bien que nous puissions obtenir plus de fonctions de réponse impulsionnelle que celles ci-dessous, nous nous concentrerons sur l’impact d’un choc de RRP sur les autres variables du système

RRPirf <- irf(Model1, impulse = "RRP", response = "RRP", n.ahead = 20, boot = TRUE)
plot(RRPirf, ylab = "RRP", main = "RRP's shock to RRP")M1irf <- irf(Model1, impulse = "RRP", response = "M1", n.ahead = 20, boot = TRUE)
plot(M1irf, ylab = "M1", main = "RRP's shock to M1")CPIirf <- irf(Model1, impulse = "RRP", response = "CPI", n.ahead = 20, boot = TRUE)
plot(CPIirf, ylab = "CPI", main = "RRP's shock to CPI")lnIPirf <- irf(Model1, impulse = "RRP", response = "lnIP", n.ahead = 20, boot = TRUE)
plot(lnIPirf, ylab = "lnIP", main = "RRP's shock to lnIP")

La commande irf () génère les IRF où nous devons spécifier le modèle, quelle sera la série d’impulsions et quelle sera la série de réponses. Nous pouvons également spécifier le nombre de périodes à venir pour voir comment l’impact ou le choc évoluera au fil du temps. Nous utilisons ensuite la commande plot () pour représenter graphiquement cet IRF. Les résultats de l’IRF sont assez déroutants. N’oubliez pas qu’une telle augmentation du RRP ne peut pas être une réaction du BSP à ce qui se passe pour les autres variables depuis qu’il a été commandé en premier. Comme vous pouvez le voir, en (a), le choc sur le RRP augmentera bien sûr le RRP, cela entraînerait alors une légère baisse de la masse monétaire (b) et une baisse de la production (d). Nous constatons également que les prix augmentent à court terme mais diminuent modérément par la suite. Selon Christopher Sims, c’est un résultat déroutant. Les résultats suggèrent que les prix augmentent après une hausse du prix conseillé. Si une contraction monétaire réduit la demande globale (lnIP) réduisant ainsi la production, elle ne peut pas être associée à l’inflation. Il poursuit en disant que le VAR pourrait potentiellement être mal spécifié. Par exemple, il pourrait y avoir un indicateur avancé de l’inflation auquel le BSP atteindra et qui a été à tort omis du VAR. Le BSP pourrait savoir que des pressions inflationnistes sont sur le point d’arriver et contrecarrer cela en augmentant le taux d’intérêt.

Si vous vous souvenez de la macroéconomie de base, une politique monétaire contractionnelle comme l’augmentation du taux directeur (taux d’intérêt) entraînera une baisse de la production. Cette baisse de la production devrait généralement peser sur l’inflation et entraîner une baisse des prix. Cependant, ce que nous voyons dans ce modèle, c’est que les prix ont augmenté, pour la plupart, ce qui est déroutant. Soi-disant, les mouvements exogènes du taux d’intérêt directeur dans l’estimation précédente n’étaient pas totalement exogènes. En d’autres termes, les chocs exogènes n’ont pas été correctement identifiés. Pour résoudre ce problème, Sims a ajouté les prix des matières premières au mélange.

Nous tournons maintenant notre attention vers la décomposition de la variance des erreurs de prévision. Encore une fois, nous pouvons retracer l’évolution des chocs dans notre système pour expliquer les variances d’erreur de prévision de toutes les variables du système. Pour ce faire, nous utilisons la commande fevd (). Comme l’IRF, nous pouvons également spécifier le nombre de périodes à venir. Dans ce cas, concentrons-nous sur RRP.

FEVD1 <- fevd(Model1, n.ahead = 10)
FEVD1
plot(FEVD1)

On voit clairement dans la fenêtre (a) que l’erreur de prévision du RRP (colonne 1) à court terme est due à elle-même. C’est le cas parce que le RRP a été placé en premier dans la commande et qu’aucun autre choc n’affecte le RRP simultanément. À des horizons plus longs, disons 10 mois, nous pouvons voir que l’IPC représente maintenant environ 16% et que la masse monétaire représente environ 2% respectivement.

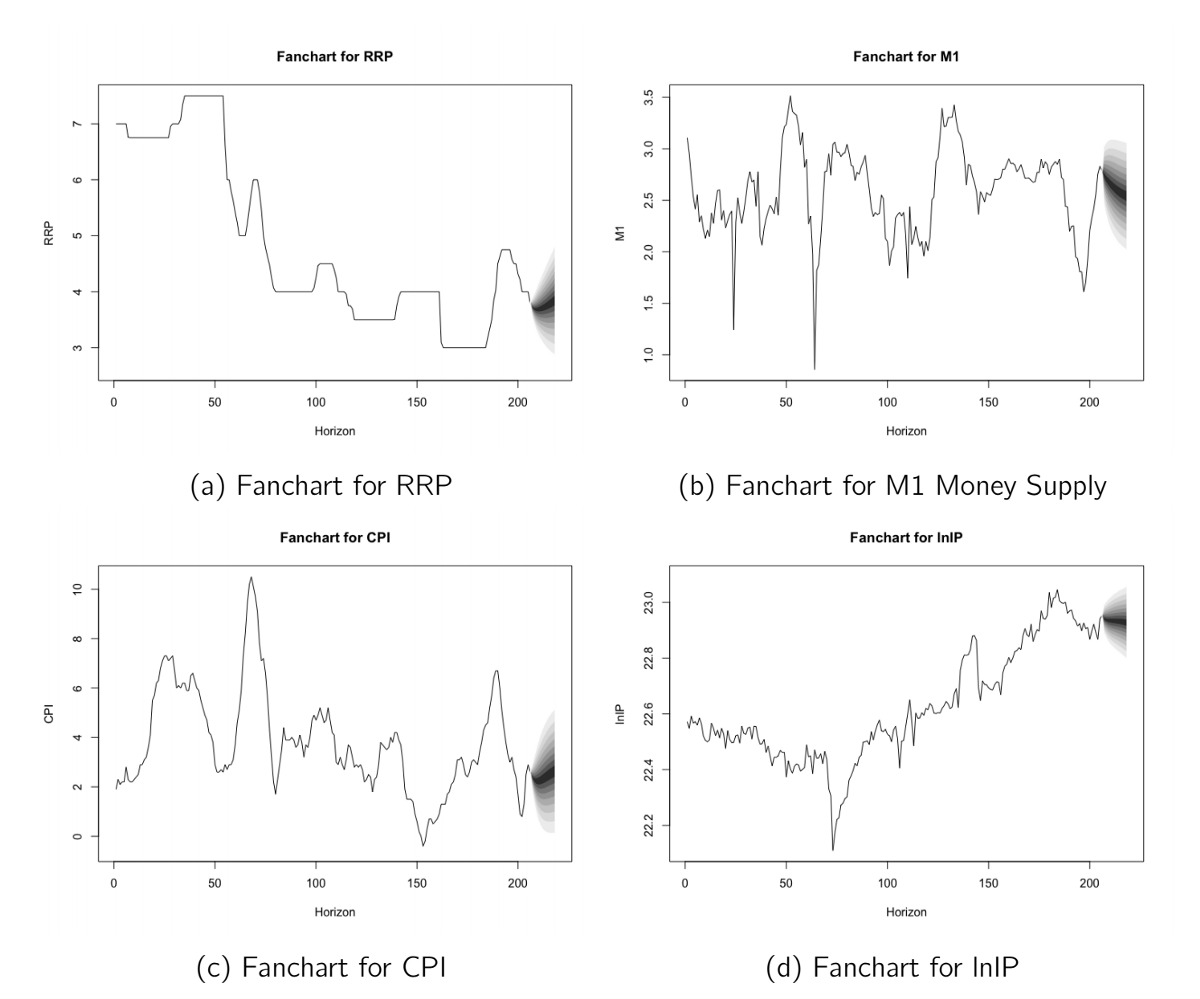
Comme nous l’avons dit, nous pouvons également prévoir en utilisant VAR. Pour ce faire, nous utilisons la commande Predict () et générons quelque chose appelé tableau des fans qui est couramment utilisé pour identifier le niveau de confiance des prévisions igraphiquement. Nous fixerons l’horizon de prévision à 12 mois à l’avance ou une prévision pour l’année entière.

forecast <- predict(Model1, n.ahead = 12, ci = 0.95)fanchart(forecast, names = "RRP", main = "Fanchart for RRP", xlab = "Horizon", ylab = "RRP")fanchart(forecast, names = "M1", main = "Fanchart for M1", xlab = "Horizon", ylab = "M1")fanchart(forecast, names = "CPI", main = "Fanchart for CPI", xlab = "Horizon", ylab = "CPI")fanchart(forecast, names = "lnIP", main = "Fanchart for lnIP", xlab = "Horizon", ylab = "lnIP")forecast

La figure montre que le RRP devrait diminuer légèrement puis augmenter, M1 devrait diminuer, tout comme IP. L’IPC devrait diminuer légèrement au cours des premiers mois, puis rebondir modérément. Notez que cela diffère des FRI simplement parce que nous utilisons le VAR comme outil de prévision au lieu d’un outil politique.

Dans l’ensemble, j’espère qu’avec cet exemple, vous pouvez voir les nombreux cas d’utilisation de la méthodologie VAR et pourquoi de nombreux économistes continuent de l’utiliser pour sa flexibilité. Outre un simple modèle de prévision, il a de nombreuses autres applications telles que la simulation de politiques, l’analyse de causalité linéaire et la décomposition des erreurs de prévision. Avant la création du VAR, l’économie avait tout épinglé sur la théorie et la pratique et croyait que les variables économiques devaient vivre selon leur code. Dans la pratique, cependant, nous savons que les variables économiques se comportent de manières qui peuvent différer de nos notions préconçues. En tant que tel, établir des attentes antérieures peut nous avoir trompés.

Pour une approche plus pratique, pensez à regarder les vidéos que j’ai faites sur ce sujet et qui sont téléchargées sur YouTube.

[1] Lütkepohl, H. Nouvelle introduction à l’analyse de séries chronologiques multiples(2005). Springer Science & Business Media.

[2] Enders, W. Séries temporelles économétriques appliquées. (2008) John Wiley & Sons.