Table des matières
Pourquoi nous avons besoin d’index pour les tables de base de données
Introduire l’indice B + Tree sans formule ni théorie informatique
Si vous n’êtes pas un DBA ou un développeur de base de données, vous ne connaissez peut-être pas les mécanismes de l’index de base de données. Mais tant que vous pouvez écrire certaines requêtes SQL, vous devez avoir entendu parler des index de base de données et savoir que les index peuvent améliorer les performances des requêtes SQL.
Dans cet article, je vais essayer d’utiliser le langage et les diagrammes les plus simples pour illustrer comment l’index d’arborescence B + peut améliorer les performances de vos requêtes SQL. La raison pour laquelle j’utilise l’index de l’arbre B + comme exemple est que
- Il est utilisé par la plupart des systèmes de gestion de bases de données relationnelles tels que MySQL, SQL Server et Oracle
- Il peut améliorer les performances de la plupart des types de requêtes SQL, plutôt que des types spécifiques
Gardons cette instruction simple, voici un diagramme simplifié illustrant la structure de l’index de l’arbre B +.
Dans l’exemple B + Tree ci-dessus, chaque rectangle représente un bloc dans le disque dur, tandis que le point bleu rempli représente un pointeur qui relie les blocs entre eux.
Veuillez noter que ce diagramme a extrêmement simplifié l’arborescence B + à des fins de démonstration, car il suppose que chaque bloc de disque dur ne peut contenir que 2 clés. En pratique, ce sera beaucoup plus important.
Il est important de comprendre comment un index d’arbre B + est construit. Il faut savoir que le niveau « Leaf Nodes » suppose d’avoir toutes les valeurs du champ sur lequel cet index a été créé. Dans l’exemple ci-dessus, il est évident que nous n’avons que 9 lignes dans cette colonne de tableau et que leurs valeurs sont comprises entre 1 et 9.
L’arbre B + peut aider la plupart des scénarios de requête de base de données, et c’est aussi la raison pour laquelle il est utile.
Requête sur un test égal
Supposons que notre requête SQL récupère à condition « égale », par exemple:
SELECT *
FROM TABLE
WHERE ID = 3
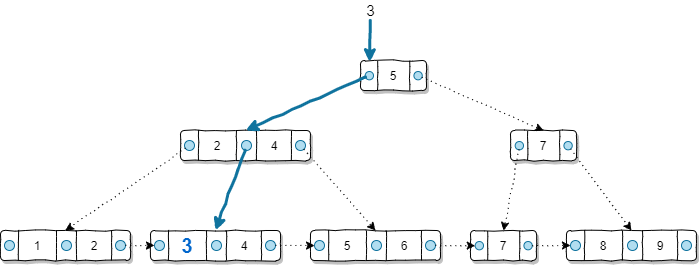
Pour trouver l’ID égal à 3, l’arborescence B + est utilisée comme suit.
- Commence à partir du niveau supérieur de l’arbre, 3 est inférieur à 5, nous devons donc utiliser le pointeur à gauche du nombre 5
- Au niveau suivant, 3 se situe entre 2 et 4, nous devons donc utiliser le pointeur au milieu
- Nous avons le bloc sur le nœud feuille, 3 est ici
Requête sur comparaison
Et si notre requête SQL recherche dans une plage? Par exemple, voici la requête SQL:
SELECT *
FROM TABLE
WHERE ID BETWEEN 3 AND 7
Voici la démonstration du processus.
- Commence à partir du niveau supérieur de l’arbre, 3 est inférieur à 5, nous devons donc utiliser le pointeur à gauche du nombre 5
- Au niveau suivant, 3 se situe entre 2 et 4, nous devons donc utiliser le pointeur au milieu
- Nous avons le bloc sur le nœud feuille, 3 est ici
- Puisque nous interrogeons sur la comparaison, le curseur continuera à chercher dans ce bloc, afin que nous puissions obtenir le nombre 4
- Nous ne sommes pas encore arrivés à 7, donc le curseur continuera d’aller au prochain bloc de nœuds feuilles (à droite)
- Nous avons atteint le bloc suivant, nous avons donc les numéros 5 et 6. Mais il n’est pas encore terminé, un mécanisme similaire à l’étape précédente sera utilisé pour accéder au bloc suivant
- Nous avons atteint le bloc suivant qui contient le numéro 7
- Nous avons atteint la limite supérieure de la plage, donc la requête est terminée
La caractéristique la plus importante des index B + Tree est qu’elle consiste en niveau du nœud feuille et niveau de clé de recherche de l’arbre.
- Toutes les valeurs de cette colonne indexée apparaissent dans les nœuds feuilles.
- Les nœuds non-feuilles ne sont utilisés qu’à des fins de recherche, il n’y a donc que des pointeurs vers le niveau inférieur. En d’autres termes, ils ne peuvent pas conduire aux entrées de données réelles.
- Chaque clé dans les nœuds terminaux a un pointeur supplémentaire vers l’entrée de données, ce qui permet au curseur de rechercher / récupérer les lignes de données.
Comme le montrent les exemples ci-dessus, B + Tree fonctionne à la fois pour des conditions «égales» et de comparaison.
Feuille c.s. Niveaux non foliaires
On peut voir que la requête n’a qu’à parcourir les clés de recherche sur les nœuds non-feuilles pour trouver les valeurs attendues. Par conséquent, lorsque la requête SQL est récupérée sur la colonne sur laquelle l’index B + Tree a été créé, seuls quelques niveaux de nœuds non-feuilles doivent passer.
Vous devez penser que les nœuds non-feuilles doivent être des sortes de frais généraux, et quand il y a beaucoup de lignes de données, cela sera ralenti car il pourrait y avoir de nombreux niveaux non-feuilles.
Partiellement correct. Oui, les nœuds non-feuilles doivent être analysés pour obtenir la valeur attendue. En fait, le nombre de fois scannées est exactement égal au nombre de niveaux non foliaires. Cependant, dans la pratique, le bloc sur notre disque dur sera beaucoup plus grand que les exemples ci-dessus. En règle générale, une table avec 10 millions d’entrées peut être placée dans une arborescence B + avec seulement 3 niveaux non foliaires. Même si le tableau est extrêmement volumineux, par exemple à l’échelle des milliards, le nombre de niveaux non foliaires de l’arbre B + est généralement de 4 ou 5.
Par conséquent, l’utilisation d’index B + Tree peut considérablement réduire le nombre de blocs de disque dur analysés dans une requête SQL.
Pourquoi le nombre de blocs numérisés est-il important?
Je suppose que le public de cet article peut ne pas avoir une formation en informatique, donc je suppose qu’une simple explication du «blocage» pourrait être nécessaire pour une meilleure compréhension du problème.
Sur notre disque dur, les données ne sont pas toujours stockées en séquence. Un seul fichier peut être divisé et stocké dans différents blocs. Ainsi, lorsque nous lisons un fichier / ensemble de données / table, afin de scanner l’ensemble du fichier, il sera nécessaire de passer d’un bloc à l’autre.
En règle générale, pour un disque dur mécanique, il existe une tête magnétique qui ne peut que monter et descendre. Lorsqu’il est nécessaire de lire des données à partir d’un emplacement différent, l’ensemble du disque dur fait pivoter l’emplacement à l’endroit où se trouve la tête magnétique afin que la tête puisse lire les données.
Imaginez que nous scannons 1000 blocs. Le pire des cas est que le disque devra être tourné 1000 fois. Si nous utilisons des index, ce nombre sera réduit à 4 à 5 fois. C’est pourquoi l’index peut contribuer aux performances.
Dans cet article, j’ai expliqué à quoi ressemble l’arbre B + et comment il fonctionne et facilite une requête SQL, généralement avec des conditions égales et comparables.
Il s’avère que B + Tree n’est plus l’index de base de données le plus avancé, mais je pense que probablement l’index le plus classique qui est toujours utilisé de manière omniprésente dans la plupart des SGBDR, c’est toujours le meilleur exemple pour démontrer pourquoi nous avons besoin d’index pour une base de données. table et comment cela fonctionne. J’espère que c’est assez intéressant pour vous.