Calculez la probabilité de vos revenus avec une seule ligne de code
Ce fait n’est qu’une conséquence de la loi des grands nombres: plus vous additionnez de choses aléatoires, mieux vous pouvez caractériser leur somme. J’aime vraiment penser à cette déclaration à l’envers:
plus les nombres sont petits, plus le hasard compte.
Cela est vrai dans les deux sens. Vous pourriez mal performer et toucher le jackpot. C’est juste de la chance.
Prenons maintenant le cas le plus courant de la vente au détail de plusieurs produits, chacun à un prix donné. En nous appuyant à nouveau sur l’exemple du peintre, par exemple, nous pourrions imaginer vendre trois types d’œuvres différentes, selon la taille: petite, moyenne et grande toile, au prix de 50 $, 100 $ et 200 $ chacune, respectivement.
nous présumer à nouveau à vendre en moyenne r= 10 œuvres d’art par mois et pour connaître la fraction dans laquelle les toiles sont généralement vendues. Par exemple, 40% petit, 40% moyen et 20% grand. Notez que ces chiffres sont tels que l’attente est inchangée par rapport au scénario à un produit. Mais qu’en est-il de la probabilité de gagner? Sera-ce sensiblement différent maintenant?
Dans ce cas précis, cela ne changera pas grand-chose. La probabilité de gagner peut à nouveau être estimée en toute sécurité avec la formule précédente, simplement en définissant une égale à la moyenne pondérée des prix des articles (une= 0,4 × 50 $ + 0,4 × 100 $ + 0,2 × 200 $).
Cependant, cela fonctionne de manière fiable tant que chaque article est vendu «assez souvent», de sorte qu’il n’y a aucun risque d’être trop proche de la zone d’incertitude des petits nombres. La formule est particulièrement précise si les prix des articles ne sont pas trop différents les uns des autres, car la moyenne est plus représentative.
Si ce n’est pas le cas ou si certains articles sont rarement vendus, il est important de dériver une formule spécifique pour ce scénario d’inventaire. Cela peut être fait au moyen du propriété d’amincissement du processus de Poisson: vendre plus de produits au taux mondial r et fraction respective Fi) est mathématiquement équivalent à vendre indépendamment chaque article je au taux r (i) = r × f (i). La formule résultante serait de toute façon conceptuellement similaire à ce qui a été montré précédemment, juste que l’on aurait besoin de additionner les rendements de tous les éléments lors du calcul du bénéfice net E
Enfin, explorons le cas le plus intéressant ici sur Medium. Comment calculer la probabilité de vos retours d’écriture?
La principale complication est que nous ne pouvons pas modéliser les revenus des histoires moyennes comme des éléments dont nous connaissons le prix à l’avance. Au lieu de cela, nous pourrions les décrire de manière probabiliste aussi en introduisant un revenir Distribution.
Nous voulons essentiellement modéliser le total des gains moyens comme la somme des retours aléatoires du nombre aléatoire d’histoires qui seront publiées dans une période de temps donnée.
La distribution de retour peut être considérée comme une version continue de la fraction de prix mentionnée précédemment. Il décrit avec quelle probabilité une histoire vous Publier par retournera un montant donné de revenus. De toute évidence, une telle distribution est spécifique à chaque auteur de Medium, car elle dépend fortement de l’expérience et de la popularité du Medium.
Pour simplifier les choses, je vais décrire ici les retours de publication avec une distribution exponentielle, pour deux raisons. Tout d’abord, cela s’applique bien à de nombreux écrivains moyens: la plupart des articles avec des rendements modestes, quelques-uns légèrement meilleurs, mais rien ne monte en flèche. Deuxièmement, la distribution exponentielle est simple car elle n’a qu’un seul paramètre, le retour moyen par poste. (Encore une fois, appelons cela une.)
Dans ces paramètres, le total des gains moyens est décrit par un processus de Poisson composé avec tarif r × t et des sommets distribués de façon exponentielle. Qu’est-ce que cela signifie concrètement? Pour commencer, regardons la valeur moyenne.
Pour le processus composé considéré, le revenu total moyen est égal à a × r × t, avec un écart type de a × sqrt (2 × r × t). le écart-type donne une idée de l’ampleur des fluctuations: les gains chuteront avec une probabilité de 68% dans un intervalle d’un écart-type au-dessus et au-dessous de l’espérance, en conséquence du théorème de la limite centrale. Cependant, pour que le théorème de la limite centrale fonctionne correctement, la règle de base est de considérer au moins plus de 20 ventes totales (c’est-à-dire des histoires moyennes, dans ce contexte).
Par exemple, si vous publiez un article par semaine et gagnez 25 $ par article en moyenne, en un an, vous vous attendez à collecter (1300 ± 255) $ (avec t= 52 semaines).
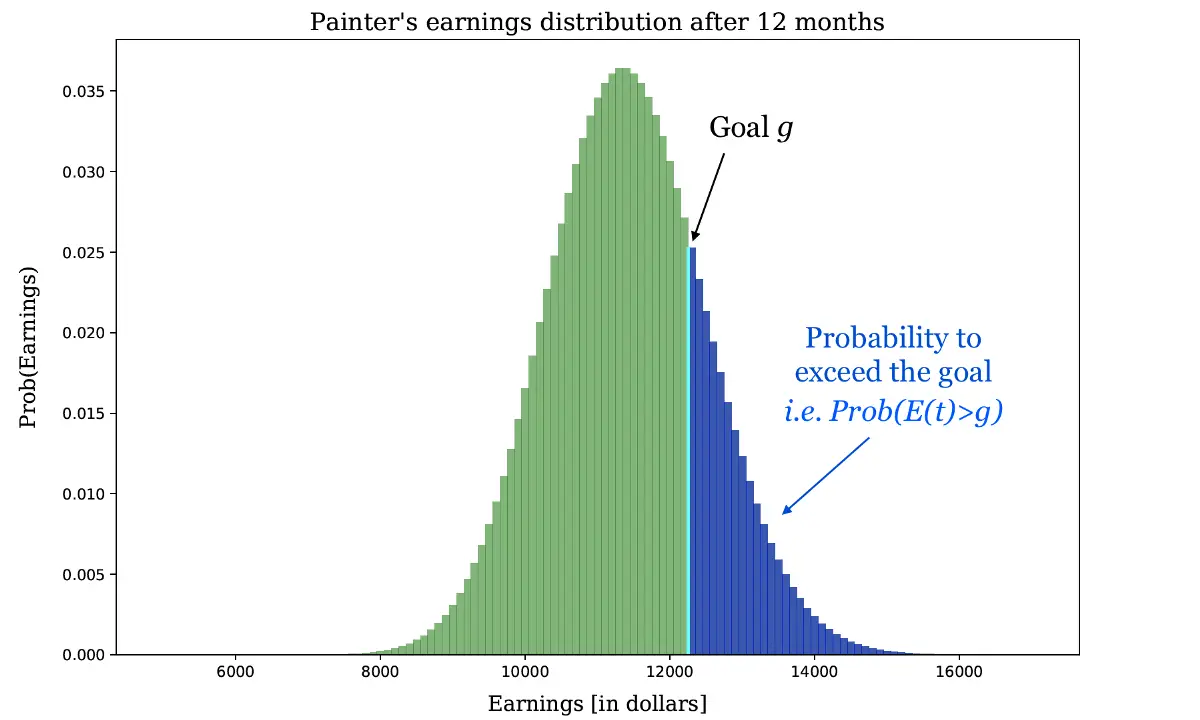
Dans le cas où vous êtes spécifiquement intéressé par la probabilité d’atteindre un objectif, la formule du peintre fonctionne également bien dans ce cas, même si ce n’est Procuration. La raison pour laquelle il est toujours valable de l’utiliser est que la distribution exponentielle n’est pas trop biaisée, comme l’exemple des prix du canevas.
Notez, cependant, que la crédibilité de la valeur de probabilité obtenue dépend de la façon dont ces hypothèses de modélisation sont respectées:
- Vous avez une bonne estimation de votre taux de publication r
- Vos gains post sont indépendants les uns des autres et distribués de façon exponentielle avec une moyenne connue une
- Rien de ce qui précède n’est modifié au cours de la période de temps t
Vous voudrez peut-être essayer la formule. Si, à la place, vous n’aimez pas les approximations, il est simple de calculer Prob (E
En Julia,
using Distributions
S = 10^6 # Number of simulations you want
p = length(findall([sum(rand(Exponential(a),rand(Poisson(r*t)))) for i=1:S] .> g)) / S
ou en Python
import numpy as np
S = 10**6 # Number of simulations you want
p = sum(map(lambda x : x > g, [sum(np.random.exponential(a,np.random.poisson(r*t))) for i in range(S)])) / S
(P.S. Julia a l’air tellement mieux et est incroyablement plus rapide. J’adore Julia!)
Le code ci-dessus résume simplement plusieurs fois un nombre de retours distribués exponentiellement distribués par Poisson. Ensuite, la probabilité de dépasser l’objectif g est simplement estimé comme la fraction des simulations dont les gains totaux sont supérieurs à g.
Mais toute cette précision est-elle vraiment nécessaire? Mais pour être honnête, probablement pas.
Le message à retenir de la théorie des probabilités appliquée à Medium confirme simplement les preuves quotidiennes: le moyen le plus robuste pour garantir votre succès sur Medium est d’augmenter votre taux de publication et d’écrire de bonnes choses. Plus une, plus ret les deux pendant plus longtemps t. Bref, plus art.
Même si je suis mathématicien, je pense que la vie est parfois plus agréable avec moins de chiffres et plus de mots. Alors bonne écriture!